
Mezunumuz Pelin Erşin'den LSE'ye Uzanan Başarı Hikayesi
İzmir Ekonomi Üniversitesi Matematik Bölümü 2024 mezunlarımızdan Pelin Erşin, dünyanın en saygın üniversiteleri arasında yer alan London School of Economics ...

İEÜ Matematik Bölümü'nden Video Destekli Eğitim: Precalculus Çekimleri Tamamlandı
İzmir Ekonomi Üniversitesi Matematik Bölümü, temel matematiksel kavramları kapsayan Precalculus dersi video çekimlerini tamamladı. Hazırlanan içerikler, öğrencilerin kendi hızlarında öğrenebilecekleri, ...

Öğrencimizden Poster Sunumunda Büyük Başarı
İzmir Ekonomi Üniversitesi Matematik Bölümü lisans öğrencilerinden Alican AKCA, Yıldız Teknik Üniversitesi Fen Edebiyat Fakültesi tarafından 21 Mayıs 2025 tarihinde ...

I. Uygulamalı Matematik ve İstatistik Çalıştayı Başarıyla Tamamlandı
İzmir Ekonomi Üniversitesi Matematik Bölümümüz tarafından düzenlenen I. Uygulamalı Matematik ve İstatistik Çalıştayı, 10 Mayıs 2025’te yoğun ilgiyle gerçekleşti. ...

Matematik Bölümü Öğrencilerimize TÜBİTAK 2209-A Araştırma Desteği!
TÜBİTAK Bilim İnsanı Destek Programları Başkanlığı (BİDEB) tarafından yürütülen “2209-A Üniversite Öğrencileri Araştırma Projeleri Destekleme Programı”nın 2024/1 dönemi sonuçları açıklandı. ...

WAMS-I.Uygulamalı Matematik ve İstatistik Çalıştayı
İzmir Ekonomi Üniversitesi Matematik Bölümü, genç araştırmacıları buluşturuyor! 10 Mayıs 2025’te düzenlenecek I. Uygulamalı Matematik ve İstatistik Çalıştayı, akademik dünyada ...

Dünya Matematik ve Pi Günü Etkinliği
Dünya Matematik ve Pi Günü, İzmir Ekonomi Üniversitesi Matematik Bölümü tarafından bu yıl yedincisi gerçekleştirilen etkinlikle kutlandı. ...
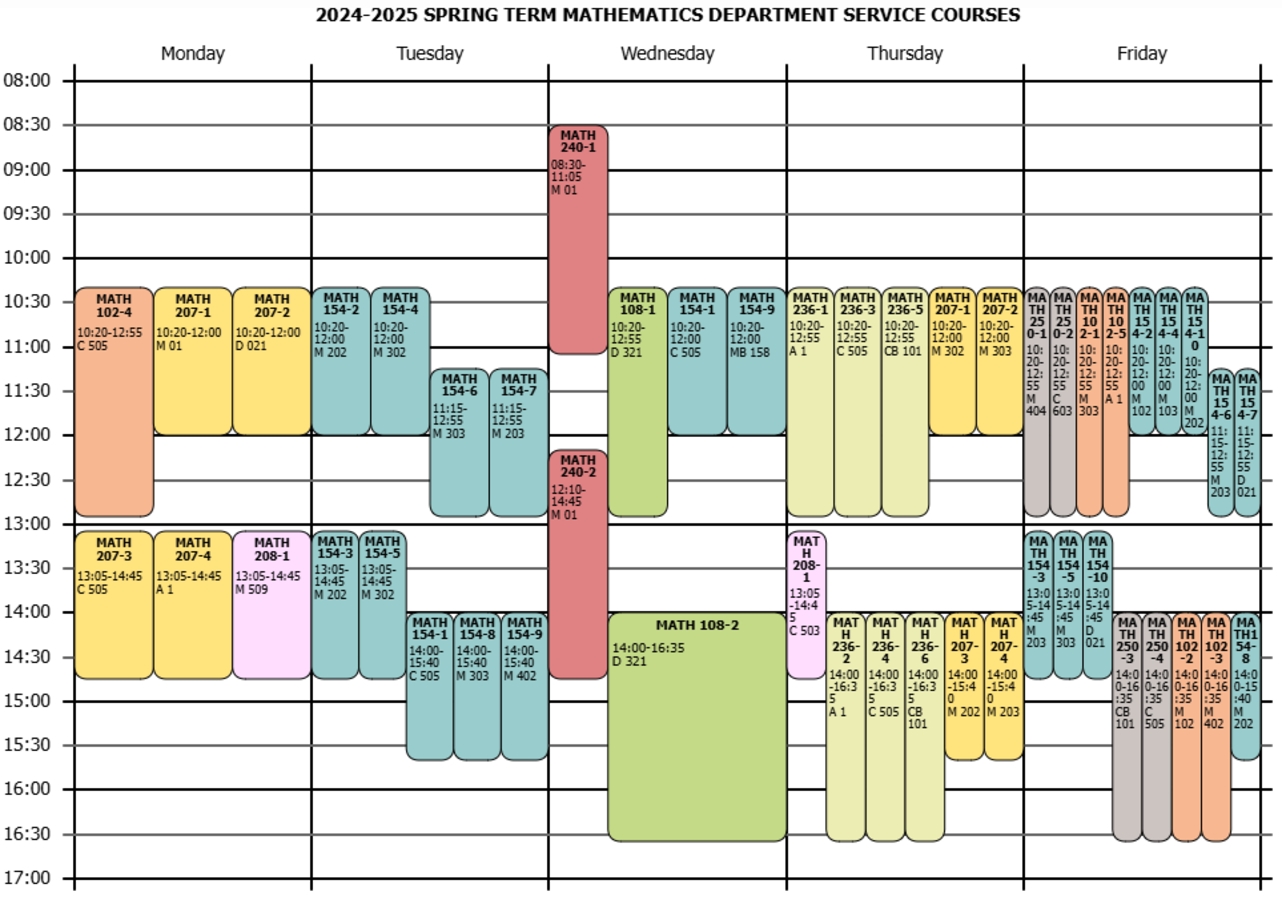
Matematik Bölümü Tarafından verilen Servis Dersleri
Matematik Bölümü Tarafından verilen Servis Dersleri ...





