
I. Uygulamalı Matematik ve İstatistik Çalıştayı Başarıyla Tamamlandı
İzmir Ekonomi Üniversitesi Matematik Bölümümüz tarafından düzenlenen I. Uygulamalı Matematik ve İstatistik Çalıştayı, 10 Mayıs 2025’te yoğun ilgiyle gerçekleşti. ...

Matematik Bölümü Öğrencilerimize TÜBİTAK 2209-A Araştırma Desteği!
TÜBİTAK Bilim İnsanı Destek Programları Başkanlığı (BİDEB) tarafından yürütülen “2209-A Üniversite Öğrencileri Araştırma Projeleri Destekleme Programı”nın 2024/1 dönemi sonuçları açıklandı. ...

WAMS-I.Uygulamalı Matematik ve İstatistik Çalıştayı
İzmir Ekonomi Üniversitesi Matematik Bölümü, genç araştırmacıları buluşturuyor! 10 Mayıs 2025’te düzenlenecek I. Uygulamalı Matematik ve İstatistik Çalıştayı, akademik dünyada ...

Dünya Matematik ve Pi Günü Etkinliği
Dünya Matematik ve Pi Günü, İzmir Ekonomi Üniversitesi Matematik Bölümü tarafından bu yıl yedincisi gerçekleştirilen etkinlikle kutlandı. ...
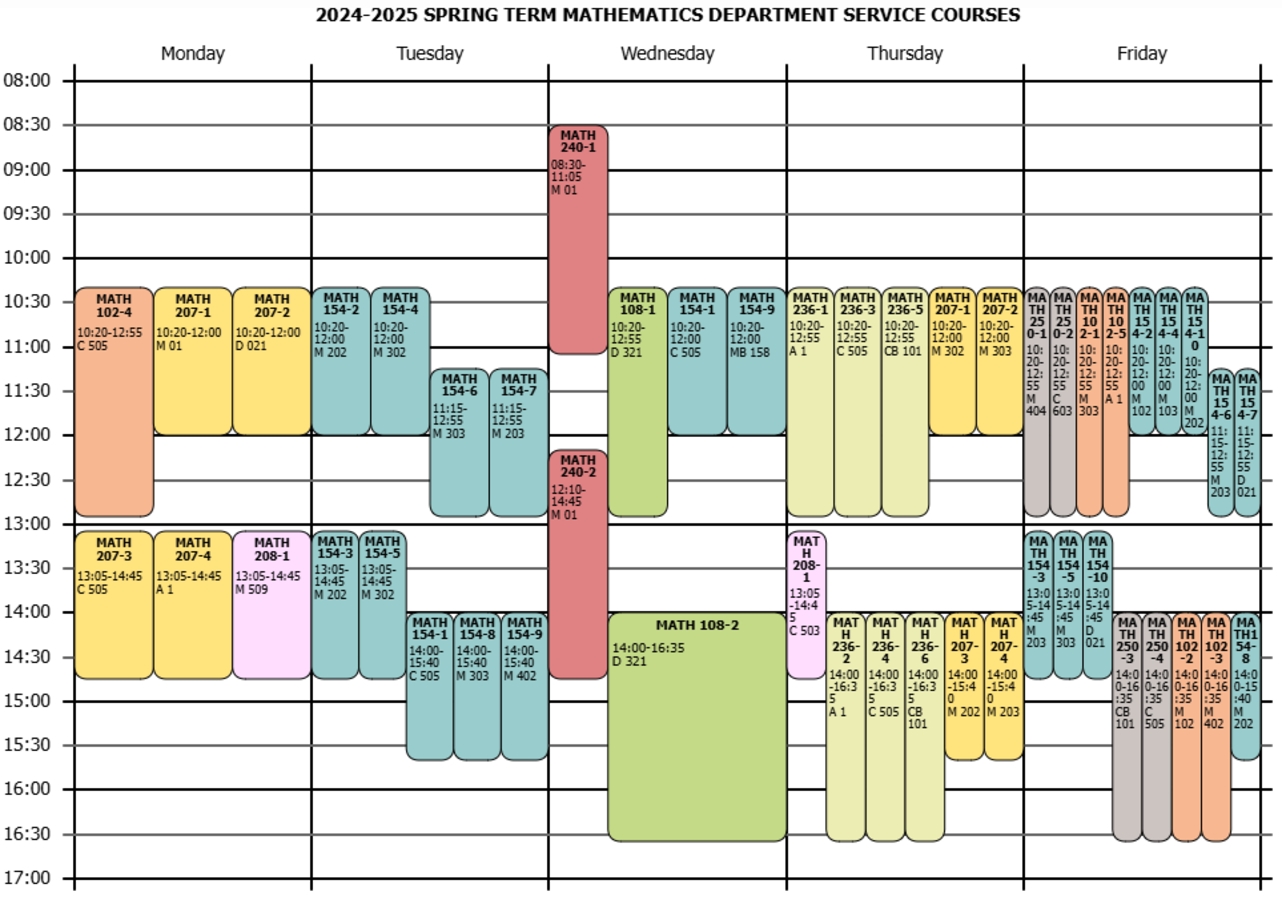
Matematik Bölümü Tarafından verilen Servis Dersleri
Matematik Bölümü Tarafından verilen Servis Dersleri ...

Prof. Dr. İsmihan Bayramoğlu "Yurt Dışında Yaşayan Azerbaycan Bilim İnsanlarının Forumu"na Katıldı
Prof. Dr. İsmihan Bayramoğlu 8-12 Eylül tarihlerinde Bakü’de, Yurt Dışında Yaşayan Azerbaycan Bilim İnsanlarının Forumuna Türkiye adına iştirak etti. ...

“CSI Education 8. Sezon Öğretmenler Toplantısı"
Bölümümüz öğretim üyeleri; üniversitemiz Rektör Yardımcısı Prof. Dr. Gözde Yazgı Tütüncü ve Araş. Gör. Dr. Ayşe Beler, İzQ Girişimcilik Merkezindeki ...

IX. Kadın Matematikçiler Derneği Çalıştayı'nı Başarıyla Tamamlandı
Misyonu kadın matematikçileri bir araya getirerek: Türkiye’de matematikle uğraşan kadınları, bilimsel ve sosyal alanlarda desteklemek olan Kadın Matematikçiler Derneği'nin bu yıl dokuzuncusu ...





